The Gounaris-Sakurai lineshape models dispersive corrections to the I=1,J=1 \(\pi\pi\) propagator (G.J. Gounaris and J.J. Sakurai, Phys. Rev. Lett.21, 244 (1968))
\[ \mathcal{A}(s) = \frac{ k(m,\Gamma_0) B_l(qr,0) }{ m^2(s) - s - i m \Gamma(s) },
\]
where the running mass \( m^2(s)\) is given by
\[ m^2(s) = m^2 + \frac{\Gamma_0}{\pi} \left( \frac{ 2 q^3 m }{q_0^3 \sqrt{s} } \log\left(\frac{\sqrt{s} + q }{ 2 m_\pi }\right) +
\frac{ q^2 ( s - 3m^2) + s(m^2-s) }{ m q_0^2 } \log\left(\frac{m+q_0}{2 m_\pi}\right) +
\frac{m^2 - s}{q_0}
\right)
\]
| Parameter | User name | Description |
| \(m\) | particleName_mass | Breit-Wigner mass, defined as energy at which the self-energy of the resonance is purely imaginary (defaults to value in PDG)
|
| \(\Gamma_0\) | particleName_width | Breit-Wigner width, defined as the width of resonance at the Breit-Wigner mass
|
| \(r\) | particleName_radius | Hadronic radius for Blatt-Weisskopf form-factor (defaults to 1.5GeV for light resonances, 3.5GeV for charm)
|
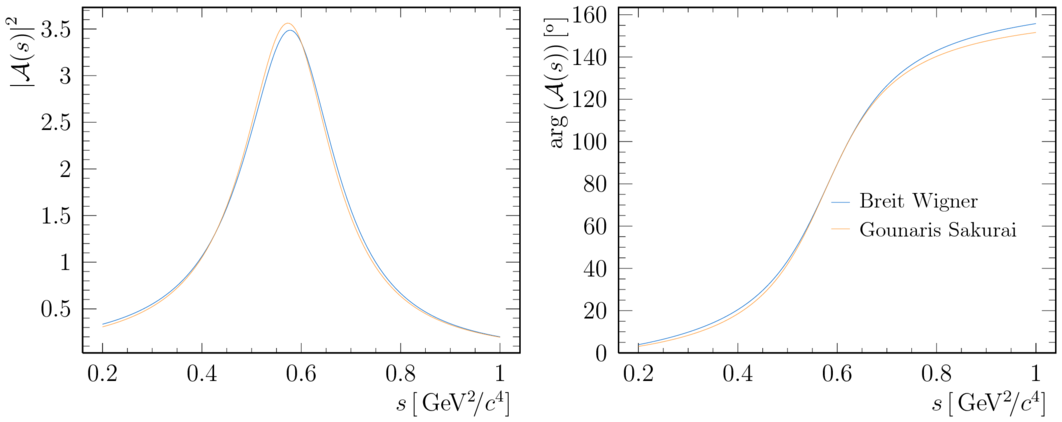
Gounaris-Sakurai lineshape for the ϱ(770) meson, with the equivalent relativistic Breit Wigner lineshape shown for comparison.
Definition at line 189 of file Lineshapes.h.