The propagator as a function of the invariant-mass squared \(s\) for a two-body final state with relative orbital angular momentum \(l\) is given by
\[ \mathcal{A}(s) = \frac{ k(m,\Gamma_0) B_l(qr,0) }{ m^2 - s - i m \Gamma_{l}(s) },
\]
where the width \( \Gamma_{l}(s) \) is given by
\[ \Gamma_{l}(s) = \frac{\Gamma_0 q m_0}{q_0 \sqrt{s}} \left(\frac{q}{q_0}\right)^{2l} B_l( qr, q_0 r )^2,
\]
where \(q\) is the linear momentum of either decay product in the rest frame of the parent, while \(q_0\) the same quantity evaluated at the resonance mass. The Blatt-Weisskopf functions, \(B_l(q,q_0)\) control the behaviour of functions at large momentum transfers. The width is normalised such that \(\Gamma(m^2) = \Gamma_0 \).
The parameters of the lineshape are tabulated below
| Parameter | User name | Description |
| \(m\) | particleName_mass | Breit-Wigner mass, defined as energy at which the self-energy of the resonance is purely imaginary (defaults to value in PDG) |
| \(\Gamma_0\) | particleName_width | Breit-Wigner width, defined as the width of resonance at the Breit-Wigner mass |
| \(r\) | particleName_radius | Hadronic radius for Blatt-Weisskopf form-factor (defaults to 1.5GeV for light resonances, 3.5GeV for charm) |
BL : Use Blatt-Weisskopf factors normalised at \( \sqrt{s}=m \) (by default, normalised at \(\sqrt{s}=0\))
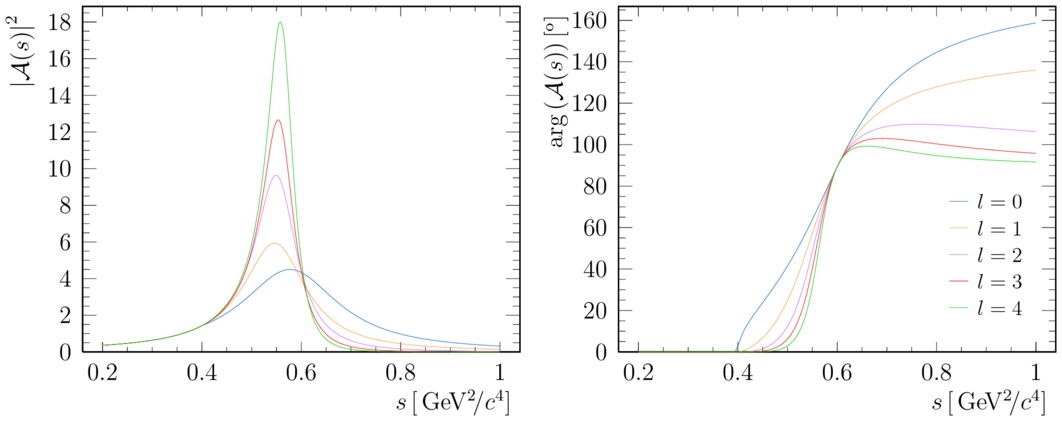
Modulus and phase of the Relativistic Breit-Wigner propagator, for orbital momentum up-to four, using the mass and nominal width of the rho meson.
Definition at line 138 of file Lineshapes.h.